The time value of money concept is the basis of finance theory. It is the idea that money now is worth more than the same amount of money in the future. The process of finding the present Value (PV) of a future cash flow is called discounting, and the interest rate at which we discount future cash flows are referred to as discount rates. In determining the discount rate for a certain cash flow, we need to consider both the risk free rate and the inflation rate, among other risk factors. The real risk-free rate is a theoretical rate with no expectation of inflation. US Treasury bills (T bills) rate is an example of nominal risk-free rate as it is already adjusted for inflation. The approximate relationship is:
Nominal risk-free rate = real risk-free rate + expected inflation rate.
If we denote the nominal interest rate per year as I/Y, the future value (FV) of the current deposit amount M after N years would be:
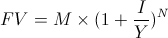
If we want to receive amount M from the bank in N years, the current deposit we need to make, i.e. the present value (PV) of the future amount M, is:
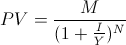
When interest is earned not only on the original principal, but also on the interest earned from the previous period, this effect is called “Compounding”. Some common compounding periods are annual, semi-annual, quarterly or monthly. The extreme case would be that the interest is earned and compounded instantly, and we call it continuous compounding.
